Ratios Of Directed Line Segments

Division a Segment in a Given Ratio

Suppose you have a line segment $\overline{PQ}$ on the coordinate plane, and you need to find the point on the segment $\frac{1}{3}$ of the way from $P$ to $Q$.

Let's first have the piece of cake case where $P$ is at the origin and line segment is a horizontal 1.

The length of the line is $\mathrm{half\; dozen}$ units and the point on the segment $\frac{1}{3}$ of the fashion from $P$ to $Q$ would be $2$ units abroad from $P$, $\mathrm{iv}$ units abroad from $Q$ and would be at $\left(2,0\right)$.

Consider the instance where the segment is non a horizontal or vertical line.

The components of the directed segment $\overline{PQ}$ are $\langle 6,3\rangle$ and we need to find the point, say $X$ on the segment $\frac{1}{\mathrm{iii}}$ of the manner from $P$ to $Q$.

So, the components of the segment $\overline{PX}$ are $\langle \left(\frac{1}{3}\right)\left(6\right),\left(\frac{1}{3}\right)\left(3\right)\rangle =\langle 2,1\rangle$.

Since the initial point of the segment is at origin, the coordinates of the bespeak $X$ are given by $\left(0+2,0+1\right)=\left(\mathrm{ii},1\right)$.

Now permit's exercise a trickier trouble, where neither $P$ nor $Q$ is at the origin.

Use the end points of the segment $\overline{PQ}$ to write the components of the directed segment.

$\begin{array}{l}\langle \left(x_2-x_{\mathrm{ane}}\right),\left(y_2-y_{\mathrm{i}}\right)\rangle =\langle \left(7-\mathrm{one}\right),\left(2-\mathrm{vi}\right)\rangle \\ =\langle 6,-4\rangle \end{array}$

Now in a similar fashion, the components of the segment $\overline{PX}$ where $X$ is a point on the segment $\frac{1}{\mathrm{iii}}$ of the mode from $P$ to $Q$are $\langle \left(\frac{1}{3}\right)\left(6\right),\left(\frac{1}{\mathrm{three}}\right)\left(-4\right)\rangle =\langle \mathrm{ii},-\mathrm{one.25}\rangle$.

To notice the coordinates of the betoken $X$ add the components of the segment $\overline{P\mathrm{10}}$ to the coordinates of the initial indicate $P$.

So, the coordinates of the bespeak $\mathrm{10}$ are $\left(\mathrm{i}+\mathrm{ii},6-\mathrm{one.25}\right)=\left(3,4.75\right)$.

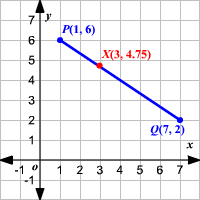
Note that the resulting segments, $\overline{PX}$ and $\overline{XQ}$, accept lengths in a ratio of $\mathrm{one}:2$.

In general: what if y'all need to find a point on a line segment that divides it into two segments with lengths in a ratio $a:b$?

Consider the directed line segment $\overline{XY}$ with coordinates of the endpoints as $X\left({\mathrm{ten}}_{\mathrm{i}},y_1\right)$ and $Y\left({\mathrm{10}}_2,y_2\right)$.

Suppose the betoken $Z$ divided the segment in the ratio $a:b$, so the betoken is $\frac{a}{a+b}$ of the mode from $X$ to $Y$.

So, generalizing the method we have, the components of the segment $\overline{\mathrm{10}Z}$ are $\langle \left(\frac{a}{a+b}\left(x_{\mathrm{two}}-{\mathrm{ten}}_{\mathrm{ane}}\right)\right),\left(\frac{a}{a+b}\left(y_{\mathrm{two}}-y_{\mathrm{i}}\right)\right)\rangle$.

So, the $X$-coordinate of the point $Z$ is

$\begin{array}{l}{\mathrm{ten}}_1+\frac{a}{a+b}\left(x_2-x_1\right)=\frac{{\mathrm{ten}}_1\left(a+b\right)+a\left({\mathrm{ten}}_2-x_1\right)}{a+b}\\ =\frac{b{x}_{\mathrm{one}}+a{x}_{\mathrm{ii}}}{a+b}\end{array}$.

Similarly, the $Y$-coordinate is

$\begin{array}{l}{y}_1+\frac{a}{a+b}\left(y_2-y_{\mathrm{one}}\right)=\frac{y_1\left(a+b\right)+a\left(y_2-y_1\right)}{a+b}\\ =\frac{b{y}_1+a{y}_2}{a+b}\end{array}$.

Therefore, the coordinates of the point $Z$ are $\left(\frac{b{x}_1+a{x}_2}{a+b},\frac{b{y}_{\mathrm{ane}}+a{y}_2}{a+b}\right)$.

Instance 1:

Observe the coordinates of the bespeak that divides the directed line segment $\overline{MN}$ with the coordinates of endpoints at $M\left(-4,0\right)$ and $\mathrm{One\; thousand}\left(0,\mathrm{iv}\right)$ in the ratio $3:\mathrm{one}$?

Permit $L$ be the signal that divides $\overline{M\mathrm{Due\; north}}$ in the ratio $3:1$.

Hither, $\left({\mathrm{ten}}_{\mathrm{ane}},y_1\right)=\left(-4,0\right),\left(x_{\mathrm{ii}},y_{\mathrm{two}}\right)=\left(0,4\right)$ and $a:b=3:1$.

Substitute in the formula. The coordinates of $\mathrm{50}$ are

$\left(\frac{\mathrm{ane}\left(-4\right)+3\left(0\right)}{3+\mathrm{ane}},\frac{1\left(0\right)+\mathrm{iii}\left(4\right)}{\mathrm{iii}+\mathrm{ane}}\right)$.

Simplify.

$\left(\frac{-\mathrm{four}+0}{\mathrm{iv}},\frac{0+12}{4}\right)=\left(-1,3\right)$

Therefore, the point $L\left(-1,3\right)$ divides $\overline{MN}$ in the ratio $3:\mathrm{i}$.

Example ii:

What are the coordinates of the point that divides the directed line segment $\overline{AB}$ in the ratio $2:3$?

Permit $C$ be the betoken that divides $\overline{AB}$ in the ratio $\mathrm{ii}:3$.

Here, $\left(x_{\mathrm{i}},y_1\right)=\left(-\mathrm{four},4\right),\left(x_{\mathrm{two}},y_2\right)=\left(\mathrm{half-dozen},-5\right)$ and $a:b=2:3$.

Substitute in the formula. The coordinates of $C$ are

$\left(\frac{\mathrm{three}\left(-4\right)+2\left(\mathrm{six}\right)}{\mathrm{five}},\frac{3\left(4\right)+2\left(-5\right)}{5}\right)$.

Simplify.

$\begin{array}{l}\left(\frac{-12+12}{5},\frac{12-\mathrm{ten}}{5}\right)=\left(0,\frac{2}{5}\right)\\ =\left(0,0.4\right)\end{array}$

Therefore, the signal $C\left(0,\mathrm{0.four}\right)$ divides $\overline{AB}$ in the ratio $2:3$.

You can note that the Midpoint Formula is a special case of this formula when $a=b=\mathrm{i}$.

Ratios Of Directed Line Segments,

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/partioning-a-segment-in-a-given-ratio

Posted by: perrybeephe1978.blogspot.com

Share this post